9. ROČNÍK – MONITOR 2006

 

1.  Vypočítajte:  33 – 52 =

     

2.  Riešte rovnicu:  x + ( x – 14 ) = 350

     

3.  Obvod obdĺžnika je 18 cm. Dĺžka jeho jednej strany je 3 cm. Aká je dĺžka jeho druhej   strany v cm?

     

4.  Marián dostal v 1. polroku z matematiky takéto známky: 1, 2, 1, 3, 1. Aký je priemer jeho známok z matematiky v 1. polroku?

     

5.  Na koľko zhodných trojuholníkov rozdelia každý trojuholník jeho tri stredné priečky?

 

6.  Z 1 800 vyrobených žiaroviek bolo 5 % chybných. Koľko vyrobených žiaroviek bolo bezchybných?

 

7.  Tabuľka udáva hodnoty priamej úmernosti medzi x a y. Určte chýbajúce číslo v tabuľke.

                                         

x

4

6

 

10

y

2

3

4

5

 

8. Vypočítajte veľkosť výšky rovnobežníka v cm na stranu a = 6 cm, keď obsah rovnobežníka je 15 cm2.

    

9.  Určte, koľko stupňov má najmenší vnútorný uhol trojuholníka ABC ak viete, že veľkosti jeho vnútorných uhlov sú v pomere α : b : g = 4 : 3 : 2

    

10. Vypočítajte a výsledok vyjadrite v základnom tvare: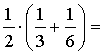  

 

11. Súčet dvoch čísel je -10,5 a rozdiel týchto čísel je 3,5. Potom súčin týchto dvoch čísel je:

      A.  24,5                       B.  49                             C.  -49                         D.  -24,5

 

12. Podielom najmenšieho spoločného násobku a najväčšieho spoločného deliteľa čísel 150 a 90 je:

     A.  60                           B.  15                             C.  42                          D.   

 

13. Útvar na obrázku je sieť kocky s objemom 8 cm3. Aký je obvod tohto útvaru?

                                                                       

      A.  28                               B.  14                         C.  38                          D.  56 

 

14. Stavebný pozemok s rozmermi 110 x 154 m určený na výstavbu rodinných domov je potrebné rozdeliť na rovnako veľké štvorcové stavebné parcely s čo najväčšou výmerou. Koľko takýchto stavebných parciel vznikne?

      A.  140                        B.  70                             C.  35                          D. 22

 

15. V žrebovacom zariadení sú štartovné čísla od 1 do 20. Aká je pravdepodobnosť, že si prvý žrebujúci pretekár v zjazdovom lyžovaní vyžrebuje štartovné číslo menšie ako 6?

      A.                          B.                              C.                             D. 

 

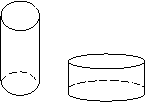
16. Valec má objem 200 litrov. Aký objem má druhý valec, ktorý je dvakrát širší a má polovičnú výšku? ( p = 3,14 )

                                                                                                                                             

      A.  200 litrov               B.  400 litrov                  C.  314 litrov                 D.  157 litrov

 

17. Riešením lineárnej nerovnice 7x + 10 > 12x – 55 sú všetky čísla, pre ktoré platí:

      A.  x < 13                        B.  x > 13                       C.  x <  – 13                    D.  x >  –13      

 

18. Osem nákladných áut odvezie na skládku za 5 pracovných dní 2 400 vriec komunálneho odpadu. O koľko viac vriec odpadu odvezie 7 áut za 7 dní?

      A.  o 980                     B.  o 540                        C.  o 2 940                  D.  o 420

 

19. Obdĺžnik PQRS je rozdelený na dva podobné obdĺžniky O1 a O2. Veľkosti menších strán týchto obdĺžnikov sú 6 cm a 3 cm. Obsah obdĺžnika PQRS je:

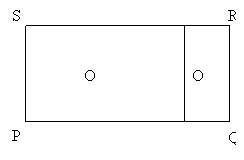
      A.  72 cm2                   B.  54 cm2                      C.  nedá sa určiť        D.  90 cm2

 

20. Určte, akú časť obsahu štvorca ABCD tvorí obsah trojuholníka AEF na obrázku.

  

   A.                              B.                              C.                             D. 

 

21. Plán televízneho štúdia je zhotovený v mierke 1 : 150. Na pláne má štúdio v tvare obdĺžnika rozmery 5 cm a 6 cm. Koľko Sk zaplatíme za pokrytie štúdia plávajúcou podlahou, ak za 1 m2 plávajúcej podlahy zaplatíme 356 Sk?

      A.  24 030 Sk              B.  11 748 Sk                 C.  19 224 Sk              D.  5 874 Sk

 

22. Trojuholník AED a rovnobežník EBCD na obrázku majú rovnaký obsah. Dĺžka strany DC je 6 m. Potom základňa AB lichobežníka ABCD má veľkosť:

      A.  90                          B.  113                           C.  135                        D.  450

 

23. Vypočítajte hodnotu výrazu ( 3a – ab ), ak a = –5, b = –0,5.

      A.  –1,8                       B.   –4,5                         C.  –17,5                     D.  –1,3

 

24. Žiaci majú vyučovanie od 8°° do 123°. Medzi vyučovacími hodinami je jedna 15-minútová a tri 10-minútové prestávky. Koľko percent vyučovania tvoria prestávky?

       A.  16,                     B.  22,5                          C.  6                                      D.   45

 

25. Riešte rovnicu:

      A.  x = –7                    B.  x =  7                        C.  x = 13                    D.  x =  2

 

26. Vo vrecúšku sú farebné guľky. Jedna tretina z nich je modrá, jedna šestina je biela, päť dvanástin je žltých a zvyšných 10guličiek je červenej farby. Koľko žltých guliek je vo vrecúšku?

      A.  20                          B.  40                             C.  50                          D.  120

 

27. Z daného vzorca vyjadrite neznámu c:

      a : b = ( b + c ) : b

      A.  c = a – b                B.  c = a + b                   C.  c = 1 – b                D. 

 

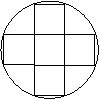
28. Do kruhovej striebornej medaile s priemerom 10 cm je vpísaný zlatý kríž, ktorý pozostáva z 5 rovnakých štvorcov. Aký je obsah zlatého kríža? ( p = 3,14 )

 

      A.  28,5 cm2                B.  78,5 cm2                   C.  50 cm2                   D.  10 cm2

 

29. Tomáš má štyri futbalové dresy: červený, modrý, biely a zelený. Koľkými spôsobmi ich môže Tomáš poukladať na policu vedľa seba tak, aby červený a modrý boli susedné? 

      A.  24                          B.12                               C.  8                            D.  6

 

 

 

 

 

 

30. Dve kružnice s polomermi 4 cm a 3 cm majú stredy vzdialené 0,5 cm. Koľko spoločných bodov majú tieto kružnice?

      A. majú práve 1 spoločný bod                             B. majú práve dva spoločné body

      C. majú viac ako 2 spoločné body                       D. nemajú žiaden spoločný bod